Piano Bar di Virginio Frigieri
Scale lineari, logaritmiche, semilogarimiche ed altro ancora… 1°parte
Prendo spunto da alcune diatribe innescate sul forum nel torrido luglio appena trascorso per cercare nel limite del possibile di dipanare l'argomento ?scale?.
Definizione di Logaritmo:
Dicesi logaritmo in base a di b, quel numero c che applicato come esponente alla base a da come risultato b.
Per chi ha un minimo di cognizioni matematiche la cosa può far sorridere.
In realtà di gente che sa esattamente cosa sono la base e l'esponente di un numero ce n'è meno di quanto si potrebbe supporre, anche se ognuno di noi quando legge un numero, usa senza rendersene conto proprio questi meccanismi.
Quindi prima di partire in quarta con l'esempio di alcuni logaritmi in base 10 che sono i più semplici, bisogna che ripercorriamo un viaggio a ritroso nel tempo fino a quando da bambini la maestra ci ha insegnato a leggere la stringa ?123' come ?centoventitrè?.
Intanto dicendo centoventitre, diamo per scontato che stiamo leggendo un numero decimale ovvero un numero in base 10.
In realtà se vi dicessi che la base di quel numero è otto al posto di dieci (sistema ottale) voi dovreste dirmi che in decimale quell' 123 ottale si legge ottantatrè, mentre se vi cambiassi ancora le carte in tavola dicendovi di leggere la medesima stringa 123 considerando il numero in base 16 (esadecimale), dovreste dirmi duecentonovantuno decimale…
Come si vede dunque, tutto è relativo.
Noi abbiamo imparato dagli arabi a ragionare in decimale ovvero a contare con un sistema numerico che contempla un insieme di dieci elementi di raffigurazione (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
Il computer al contrario ragiona solo in binario ovvero con un sistema numerico che contempla un insieme di due soli simboli (0, 1).
Il sistema di numerazione ottale si chiama così perché contempla un insieme di otto simboli di raffigurazione (0,1, 2, 3, 4, 5, 6, 7).
Il sistema esadecimale infine ne contempla addirittura 16 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Tornando all'esempio iniziale, quando voi, d'istinto vedendo ?123?, dite centoventitrè, avete compiuto un complesso processo di calcolo che ha del miracoloso e la dice lunga sulle capacità di quella sofisticatissima macchina che è il nostro cervello…
Il nostro cervello legge centoventitrè perché attribuisce pesi differenti a ciascun numero in funzione della sua posizione… è una cosa che abbiamo imparato a fare meccanicamente da bambini e ci viene quindi naturale ma in realtà è molto complessa.
Quindi il 3 che è la cifra più a destra prende peso zero (0), il 2 nel mezzo prende peso uno (1) e l'uno più a sinistra prende peso due (2)… se vi fosse una quarta cifra prenderebbe peso 3 e così via.
Questi pesi in matematica si chiamano esponenti e vanno applicati alla relativa base di numerazione che per il sistema decimale è dieci (10).
A questo punto ecco il percorso completo che il nostro cervello ha fatto nell'attimo in cui abbiamo detto centoventitre:
3 × 10º = 3
tutti i numeri elevati alla zero danno 1 (uno) e quindi 10 elevato alla 0 non fa eccezione , e da qua la maestra ci ha insegnato che la cifra più a destra di un numero decimale rappresenta le unità.
2 × 10¹ = 20
infatti 10 elevato alla 1 fa 10 e da qua la maestra ci ha insegnato che le cifre in penultima posizione partendo da destra in un numero decimale rappresentano le decine.
1 × 10² = 100
infatti 10 elevato alla 2 fa 100 e da qua la maestra ci ha insegnato che le cifre in terz'ultima posizione partendo da destra rappresentano le centinaia e così via…
Quindi 100+20+3 = 123 centoventitrè!…
Alcuni esempi in base diversa da 10 vi permetteranno di imparare rapidamente a contare in qualunque base:
convertiamo 3FA5 (esadecimale) in decimale.
Ora la base è 16 mentre gli esponenti (pesi) vanno sempre da zero per la cifra più a destra a crescere di uno mentre ci si sposta a sinistra:
pertanto ripetendo il giochino già visto per il 123 avremo:
5 × 16º = 5
A x 16¹ = 160 (A esa segue il simbolo 9 ed equivale a 10 dec)
F x 16² = 3840 (F esa equivale a 15 dec)
3 × 16³ = 12288 (3 esa equivale a 3 dec)
Quindi 12288+3840+160+5=16293 dec.
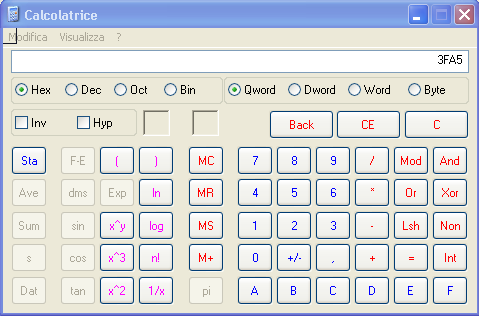
Faccio notare che potete rapidamente verificare questi calcoli con la calcolatrice di Windows impostata in visualizzazione scientifica:
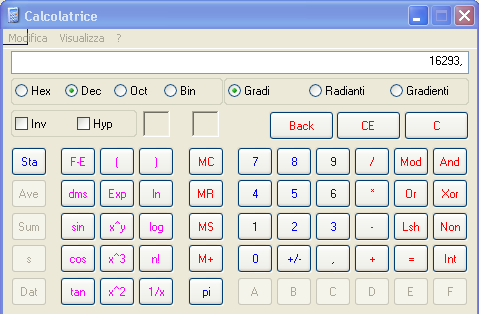
Cliccate sul pallino Hex e digitate 3FA5 con il tastierino, quindi cliccate sul pallino Dec e deve comparirvi 16293.
Ora convertiamo 777 ottale in decimale:
Sempre con lo stesso giochino ripetuto fino al rincoglionimento avremo:
7 × 8º = 7
7 × 8¹ = 56
7 × 8² = 448
Quindi 448+56+7=511 dec.
Ancora una volta potete verificare con la calcolatrice di windows
Per finire convertiamo 1110 da binario a decimale:
Ripetiamo il giochino (qua la base è 2) sempre da destra verso sinistra ed avremo:
0 × 2º = 0
1 × 2¹ = 2
1 × 2² = 4
1 × 2³ = 8
Quindi 8+4+2+0 = 14 dec.
Un po' più lungo sarebbe spiegare il percorso inverso da un numero decimale a binario ottale o quel che volete, ma fortunatamente qua non ci serve.
Ora che è ben chiaro cosa è la base e cosa è l'esponente riprendiamo la definizione iniziale:
Dicesi logaritmo in base a di b, quel numero c che applicato come esponente alla base a da come risultato b.
Premesso che le basi dei logaritmi come quelle dei numeri possono essere tante, diciamo per semplificare che parlando di logaritmi le basi più diffuse in assoluto sono tre:
Log in base 10
Log in base 2
Log in base e (e è il numero di Nepero =2,71828182845904523536…)
Allora:
il Log 10 = 1 poiché la base 10 elevata alla 1 = 10
¹º
il Log 100 = 2 poiché la base 10 elevata alla 2 = 100
¹º
il Log 1000 = 3 poiché la base 10 elevata alla 3 = 1000 e così via…
¹º
Terminato questo lungo preambolo sulla base (n°di simboli) e l'esponente (peso) dei diversi sitemi di numerazione, passiamo finalmente andare a parlare dei grafici.
La rappresentazione grafica di una generica funzione y=f(x) richiede tipicamente due assi ortogonali sui quali si riportano i valori della x (asse orizzontale) e della y (asse verticale).
Ogni asse deve essere graduato, ovvero suddiviso in tanti valori numerici (o tacche se preferite) e tale suddivisione prende il nome di scala graduata.
La scelta della scala, è arbitraria e dipende dall'intervallo di valori da rappresentare per ciascuna variabile.
La scala più diffusa è sicuramente la scala lineare dove la distanza tra due tacche consecutive è costante per incrementi costanti del valore assoluto di x e di y.
Il maggiore inconveniente nell'utilizzo della scala lineare si ha quando le grandezze da rappresentare sul grafico hanno una grande variabilità con escursioni molto ampie di valori.
Per sopperire a questi inconvenienti e migliorare la leggibilità del grafico si è allora costretti a ricorrere a scale non lineari.
Fra queste la scala più diffusa è sicuramente la s
