Buon pomeriggio a tutti,
come vi avevo anticipato qualche giorno fa, riprendo l'argomento degli open interest, del maximum pain e del put call ratio, per spiegarvi l'ultimo tassello del mio lavoro. Buona lettura!
Ricorderete che nell'articolo sull'hedging vi avevo detto che i grandi speculatori quando hanno opzioni vendute le cui basi vengono oltrepassate si coprono dal rischio utilizzando il sottostante in misura proporzionale al delta. Così, riprendendo un esempio fatto in precedenza, delle 100 call vendute con uno strike che è stato oltrepassato, se il delta di quelle call è pari a 0,60 allora 60 di quelle call sono diventate delle put sintetiche e 40 sono rimaste call.
Questo come incide sul maximum pain? Ovviamente incide in modo forte, perchè se prima la soglia dello strike delle call vendute era una barriera di resistenza ora diventa una barriera di supporto secondo un fattore 20. Perchè 20? Perchè 60 sono le call che sono diventate put sintetiche, 40 sono le call che sono rimaste call, quindi 40 put e 40 call si bilanciano, e rimangono 20 put sintetiche a spingere verso l'alto.
E' tutta una questione di bilancio quindi: bilancio tra call e put vendute, ma tenendo conto anche delle inversioni di tipo dovute alle coperture.
E ovviamente non vi sarà sfuggito che cambia anche il conteggio del put/call ratio!
Questo è il lavoro che io ho fatto negli ultimi tempi, culminato nel programma di cui vi ho parlato precedentemente. Premetto che il mio programma è in effetti una semplice macro di excel, che prende i dati degli open interest (vi ricordo che faccio un copia/incolla dalla quick trade di iwbank) e li elabora in funzione di alcune fasi precise: accodamento, analisi e calcolo di maximum pain e put call ratio secondo i criteri standard, spostamento delle posizioni hedgiate, ricalcolo dei maximum pain e dei put call ratio. Ho usato il plurale in quest'ultima parte perchè di maximum pain e di put call ratio 'corretti' io ne calcolo due. Il primo è basato sull'ipotesi dell'hedging minimo, ossia dell'hedging delle sole posizioni in the money, per massimizzare l'utile; il secondo è basato invece sull'ipotesi dell'hedging totale (rileggetevi l'articolo "hedging – parte seconda" del 16/2 se vi state perdendo).
Un problema che ho dovuto affrontare è stato il calcolo del delta. Il delta non è difficile da calcolare come formula (soprattutto per un foglio excel), ma richiede l'inserimento di molti input di base (sottostante, strike, scadenza, volatilità implicita, tasso di interesse, dividendi e relative date di pagamento) e qui sorgono altri problemi, specialmente per quanto riguarda il valore della volatilità implicita…
Ma alla fine di tutto il mio personale obiettivo non era quello di ottenere un modello perfetto (poi capirete perchè), bensì verificare se fosse possibile ottenere una stima migliore del maximum pain (quello standard a volte prende delle vere e proprie cantonate), pur basandosi su un modello approssimativo.
Così ho impostato un modello fisso di delta, con tutte le limitazioni che un simile approccio comporta. Tanto per rendere l'idea, il delta ha genericamente un grafico ad "S", con un centro intorno a 0,50 intorno allo strike at the money. Ma questo vale in condizioni di mercato nomale, a circa un mese di distanza dalla scadenza e con una volatilità implicita 'normale'. In condizioni di alta volatilità implicita il grafico del delta tende a diventare una linea retta inclinata a 45 gradi con un valore mediano, 0,50, molto più spostato verso gli strike lievemente out of the money (in alta volatilità infatti anche opzioni out of the money hanno una probabilità molto maggiore di finire in the money)…. quando la vita residua si accorcia molto il grafico del delta cambia di nuovo… insomma, uno può infarcire il modello fin che gli pare, ma se non calcola in modo puntuale i delta avrà comunque risultati approssimativi…
Quindi io ho risolto il problema assumendo un modello approssimativo di delta. L'approssimazione, almeno per me, è più che tollerabile: se infatti, per fare un esempio, sbaglio il delta di 0,1 (e già è un errore grossolano, che il mio modello non dovrebbe commettere se non in situazioni limite) allora ogni 100mila opzioni da convertire ne converto 10mila in più o in meno. E su un sottostante come l'Eurostoxx, sul quale alle scadenze trimestrali ci sono 4-5 milioni di opzioni aperte non sono di certo le mie 10mila in più o in meno che sballano il computo!
Ma la ragione principale è un'altra, ed è quella che mi ha convinto a desistere da qualsiasi velleità di raggiungere o anche solo avvicinare la perfezione: il valore del maximum pain ricalcolato con il mio modello ha un ridottissimo valore previsivo (pochi giorni). A che pro quindi diventare matti per ricavare un valore talmente preciso che fra un'ora sarà già cambiato? Maggiore è il livello di precisione del ricalcolo, infatti, minore è la sua longevità!
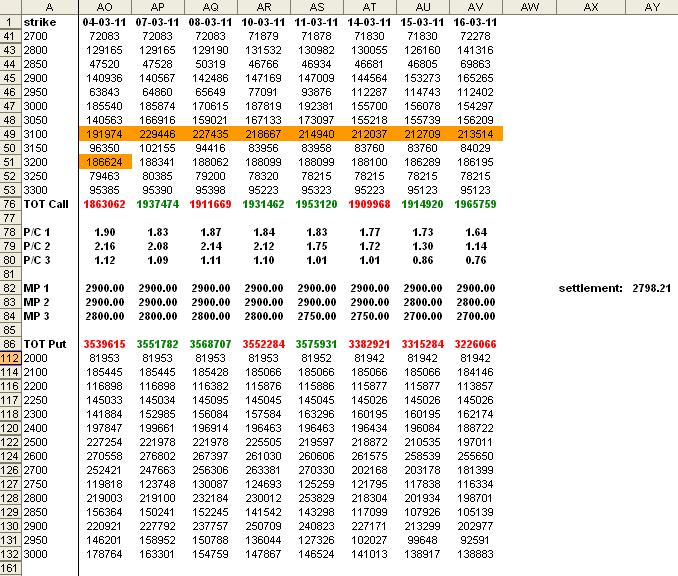
Tanto per darvi una idea, quella che segue è la situazione che si aveva su Eurostoxx la scorsa settimana, a ridosso delle scadenze di marzo (nota: il giorno 17 è mancante perchè nel giorno di scadenza la quicktrade non fornisce gli open interest):
concentratevi sulle righe centrali, quelle dei Put/Call ratio (P/C) e dei maximum pain (MP). Le righe 1 (cioè P/C 1 e MP 1) riportano i valori calcolati secondo il metodo standard, quindi senza alcuno spostamento di opzioni. Le righe 2 sono determinate secondo il modello dell'hedging parziale. Le righe 3 sono determinate secondo il modello dell'hedging totale.
Vedete come è più preciso il modello dell'hedging parziale? ha pronosticato un maximum pain a 2800 punti contro i 2900 del modello standard, e la scadenza è poi stata 2798 punti. Ma vedete anche che questa informazione era disponibile soltanto da due giorni, mentre prima era in linea con il computo standard, quindi errata!
In fondo il maximum pain è sostanzialmente il baricentro del mercato; in quanto tale non può essere calcolato su valori futuri, per definizione… Ecco perchè ritengo inutile spingermi oltre con il modello di calcolo: cui prodest? In fondo il problema principale non è che il valore del MP sia preciso, ma che non sia piuttosto molto sbagliato; e il punto è che a volte non basta guardare agli open interest per vedere a colpo d'occhio dove sia il baricentro, perchè possono esserci posizioni fortemente sbaricentrate che spostano sensibilmente l'ago della bilancia, da cui la necessità di un calcolatore più o meno preciso.
Altro dato interessante: a fronte di un put call ratio di 1,64 secondo il computo standard, il put call ratio ricalcolato in funzione dell'hedging parziale è pari a 1,14; ciò ci dice che la spinta rialzista 'reale' era molto più bassa di quella che appariva dai dati puri. Ma è anche vero che questa minore forza è diventata chiara soltanto alla fine del periodo, quindi di nuovo abbiamo uno scarso valore previsivo.
I conteggi alle righe 3 sembrerebbero da buttare, ma in realtà ho notato più di una volta che hanno un altro utilizzo, molto utile. Devo però ancora verificare sul campo questa estensione del mio lavoro, perciò per ora non me la sento di sbilanciarmi.
Al solito, se vi siete persi e volete chiarimenti non fatevi scrupoli.
Domenico
